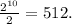Question

Determine the dynamic range for a 10-bit sign-magnitude pcm code.

Answer 1

Final Answe

rThe dynamic range for a 10-bit sign-magnitude PCM code is
`\( (2^(10))/(2) \) or 512.`

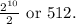
Explanation

In PCM (Pulse Code Modulation), a 10-bit sign-magnitude code signifies 10 bits used for encoding, where the most significant bit (MSB) indicates the sign (positive or negative) and the remaining 9 bits represent the magnitude.

The total number of possible combinations for a 10-bit code is
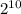`\(2^(10)\)`which equals 1024.

However, in sign-magnitude encoding, half of these combinations are utilized for negative values (due to the sign bit).

Therefore, the usable dynamic range is reduced by half, resulting in
`\( (2^(10))/(2) = 512 \).`

Answer 2

For a 50-dB hearing loss, sounds must be amplified by
`10^5` times the original intensity for them to be perceived as normal, with the caveat that more intense sounds require less amplification.

Step-by-step explanation:

To determine how much amplification is needed for a 50-dB hearing loss, we use the fact that every 10-dB increase corresponds to a factor of 10 in sound intensity. So, for a person with a 50-dB hearing loss to perceive sounds as normal, the sounds need to be amplified by five factors of 10, which is
`10^5` times the original intensity. It is important to note that smaller amplification is needed for more intense sounds to avoid further hearing damage; thus, the amplification should be adapted to the intensity level of the sound.