Question

A flat screen television is advertised as being 56 inches on its diagonal. If the TV is 17 inches tall, then how wide is the screen?

Answer 1

• 53.36

Given :

• Diagonal : 56 inches
• Length : 17 inches

To find :

• Width of the screen

Solution :

We know that,

• 
  `d = \sqrt{ \\ (l {}^(2) + w {}^(2) }`

wherein,

• d = diagonal
• l = length
• w = width

Plugging in the values of diagonal and that of the length,

• 
  `56in = \sqrt{ {(17in)}^(2) + w {}^(2) }`
• 
  `(56in) {}^(2) = (17in) {}^(2) + w {}^(2)`
• 
  `w {}^(2) = (56in) {}^(2) - (17in) {}^(2)`
• 
  `w {}^(2) = 3136in {}^(2) - 289in {}^(2)`
• 
  `w {}^(2) = 2847in {}^(2)`
• 
  `w = \sqrt{2847in {}^(2) }`
• 
  `w = 53.36in`

Therefore,the width of the screen would be equal to 54.36 inches (2 d.p.) .

Answer 2

53.36 inches

Explanation:

Given:

For television:

Diagonal of rectangle (Television) = 46 in

Height = 17 in

To find:

Wide of the television(w) = ?

Solution:

In order to find the width of the screen, we can use the Pythagorean Theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

In this case, the hypotenuse is the diagonal of the TV, which is 56 inches. One of the other sides is the height of the TV, which is 17 inches. We want to find the length of the other side, which is the width of the screen.

So, we can set up the following equation:

`\sf Diagonal^2 = Height^2 + width^2`

`\sf 56^2 = 17^2 + w^2`

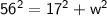
where w is the width of the screen.

`\sf 3136 = 289 + w^2`

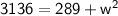
Isolate w².

`\sf w^2 = 3136 - 289`

`\sf w^2 = 2847`

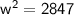
Take a square root in both sides

`\sf w = √(2847)`

`\sf w \approx 53.36 \textsf{( in 2 d.p.)}`

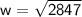
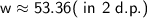
Therefore, the width of the screen is approximately 53.36 inches.