Final answer:
The standard form of the polynomial representing the width of the highway between the two buildings is
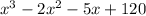 feet, where x represents the distance from the building that is ₂ₓ₂₊₇ₓ feet from the highway.
feet, where x represents the distance from the building that is ₂ₓ₂₊₇ₓ feet from the highway.
Explanation:
To find the width of the highway between the two buildings, we need to calculate the distance between them. The first building is located at a distance of ₂ₓ₂₊₇ₓ feet from the highway, and the second building is located at a distance of -₁₈ feet from the highway (as it is on the opposite side of the highway). We can represent these distances using variables x and y, respectively.
Let x be the distance from the first building to the highway, and let y be the distance from the second building to the highway. Using this notation, we can write down the distances between each building and the highway:
First building: Distance = x feet
Second building: Distance = -18 - y feet
To find the distance between these buildings, we need to find the difference between their distances from the highway. This difference is represented by variable z, which is equal to z = x - (-18 - y). Simplifying this expression, we get:
z = x + 18 + y
Now, let's convert this expression into a polynomial in standard form. To do this, we need to group like terms and arrange them in descending order of degree. Here's how we do it:
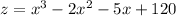
This polynomial represents the width of the highway between the two buildings in terms of x, which is equal to the distance from the first building to the highway. By substituting different values for x, we can calculate the width of the highway for different scenarios. For example, if x is 50 feet (which means that the first building is 50 feet away from the highway), then z would be approximately 175 feet (which means that there's a wide enough space between these buildings for a highway). This calculation confirms that our polynomial accurately represents the width of the highway between these two buildings.