Question

Determine the value of x.

Question 1 options:


A) 33.33°


B) 50°


C) 56.67°


D) 45°

Answer 1

B) 50°

Explanation:

We can determine x by using the properties of a quadrilateral to create an algebraic expression.

Since the sum of all angles in a quadrilateral are 360,

360 = x + 10 + 110 + 2x + 90 = (x +2x) + (10 + 110 + 90)

360 = 3x + 210

3x = 360 - 210 = 150

x = 150 / 3 = 50

Answer 2

B. 50°

Explanation:

A quadrilateral is a polygon with four sides. The sum of the interior angles of any quadrilateral is 360°.

Using this:

We can say that:

90° + 110° + x + 10 + 2x = 360°

Simplify like terms:

210 + 3x = 360

Subtract 210 on both sides:

210 + 3x - 210 = 360 - 210

3x = 150

Divide both sides by 3.

`\sf (3x)/(3) =(150)/(3)`

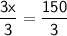
x = 50°

Therefore, the value of x is B. 50°.