Question

A line contains points (9,-30) and (-1, -32). Which Equation represents the line that is perpendicular to the given line and passes through point (3,-12)

Answer 1

y = -5x + 3

Explanation:

First, the slope is 1/5, but we want a perpendicular line so the slope is now -5.

Second, we will use this equation y - y(1) = m (x - x(1)). Here, we are using (3, -12) so we will substitute in and complete the equation like so:

y - (-12) = (-5) (x - (3))

y + 12 = -5x + 15

- 12 - 12

y = -5x + 3

Answer 2

We need to determine the slope of the line through (9,-30) and (-1,-32).

`(x_1,y_1) = (9,-30) \text{ and } (x_2,y_2) = (-1,-32)\\\\m = \text{slope} = \frac{\text{rise}}{\text{run}} = \frac{\text{change in y}}{\text{change in x}}\\\\m = \frac{\text{y}_(2) - \text{y}_(1)}{\text{x}_(2) - \text{x}_(1)}\\\\m = (-32 - (-30))/(-1 - 9)\\\\m = (-32 + 30)/(-1 - 9)\\\\m = (-2)/(-10)\\\\m = (1)/(5)\\\\`

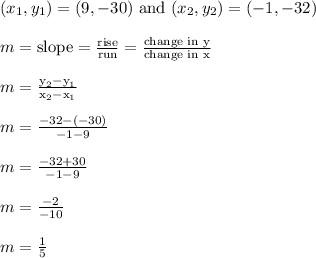
The slope is 1/5. It means "go up 1, then go right 5".

Then we apply the negative reciprocal. Flip the fraction to go from 1/5 to 5/1 aka 5.

Then flip the sign to go from +5 to -5.

• Original slope = 1/5
• Perpendicular slope = -5

The two slopes multiply to -1.

Now we use point-slope form with the given point (3,-12) and the perpendicular slope we just calculated.

`y - y_1 = m(x - x_1)\\\\y - (-12) = -5(x - 3)\\\\y + 12 = -5(x - 3)\\\\y + 12 = -5x + 15\\\\y = -5x + 15 - 12\\\\y = -5x + 3\\\\`

This is the perpendicular line to the line through (9,-30) and (-1,-32); and this perpendicular line passes through (3,-12).

As a way to confirm this, you can use Desmos or GeoGebra as a graphing tool.

Final Answer: y = -5x + 3