Answer:
Answer is E
Explanation:
To find the length of the line segment with endpoints W(5, -3) and X(-1, -9), you can use the distance formula, which is derived from the Pythagorean theorem in two-dimensional space. The distance formula is:
![\[d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yn44hako9l7ryyxm2wqp1dwuet5dzxeggo.png)
In your case,
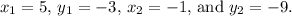 Plug these values into the formula:
Plug these values into the formula:
![\[d = √((-1 - 5)^2 + (-9 - (-3))^2)\]](https://img.qammunity.org/2024/formulas/mathematics/college/tsho8pism4ricnk12s7bdsxnpvaztd2ovl.png)
Now, simplify the expression inside the square root:
![\[d = √((-6)^2 + (-6)^2)\]](https://img.qammunity.org/2024/formulas/mathematics/college/m9aq2ngf7tnkz5pente4may0gycg9ipypz.png)
![\[d = √(36 + 36)\]](https://img.qammunity.org/2024/formulas/mathematics/college/nx361qv87it5cx0160mwj0ae1x899irnvi.png)
![\[d = √(72)\]](https://img.qammunity.org/2024/formulas/mathematics/college/i7g1n4xzf2plywfx5i960rvhaoli31l38b.png)
Since
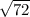 is equal to
is equal to
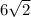 , the length of the line segment WX is
, the length of the line segment WX is
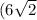 units.
units.