Question

2

A graphic design agency is making logos
of different sizes for a company. The logo
consists of a square and two semicircles.
(See the picture)
-1
Find A¹ (x)
and explain
its meaning
A¹(x)=

Answer 1

`A^(-1)(x)=(2√(4 +\pi)√(x))/(4 +\pi)`

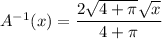
Explanation:

The area of the logo consists of a square and two congruent semicircles, where the side length of the square is equal to the diameter of the semicircles.

Let A(x) represent the area of the logo, and x be the side length of the square. Since the radius of a semicircle is half its diameter, the radius of the semicircle is x/2.

As there are two congruent semicircles, their combined area is equal to the area of a circle. Therefore, the area of the logo is the sum of the area of a square and the area of a circle:

`A(x) = x^2 + \pi\left((x)/(2)\right)^2`

`A(x) = x^2 + (\pi x^2)/(4)`

`A(x) = \left(1 + (\pi)/(4)\right)x^2`

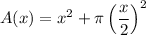
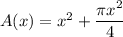
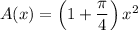
A⁻¹(x) is the inverse of A(x). To find A⁻¹(x), swap x and y and then solve for y:

`x = \left(1 + (\pi)/(4)\right)y^2`

`(x)/(1 + (\pi)/(4)) = y^2`

`y^2=(4x)/(4 +\pi)`

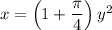
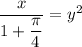
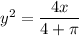
Take the positive square root, since area and length are positive:

`y=\sqrt{(4x)/(4 +\pi)}`

`y=(√(4x))/(√(4 +\pi))`

`y=(2√(x))/(√(4 +\pi))`

`y=(2√(x))/(√(4 +\pi))\cdot (√(4 +\pi))/(√(4 +\pi))`

`y=(2√(4 +\pi)√(x))/(4 +\pi)`

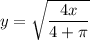
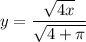
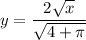
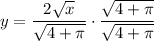
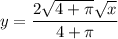
Therefore:

`A^(-1)(x)=(2√(4 +\pi)√(x))/(4 +\pi)`

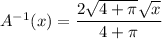
A⁻¹(x) allows us to find the side length of the square when we know the area of the logo, with "x" representing the area of the logo.

For example, if we know that the area of the logo is (4 + π) square units, we can substitute x = (4 + π) into A⁻¹(x), and the result will provide us with the side length that corresponds to that specific area.