Question

Determine the measure of an exterior angle of a regular 20-gon.

A)3,240°


B)3,600°


C)360°


D)18°

Answer 1

We know

sum of exterior angles =360°

Now

• no of sides=n=20

So measure of one exterior angle is

• 360/n
• 360/20
• 18°

Answer 2

D) 18°

Explanation:

The Exterior Angle Sum Theorem states that for any convex polygon, the sum of the exterior angles is always equal to 360°.

Therefore, to find the measure of an exterior angle of a regular polygon, we can use the following formula:

`\boxed{\begin{array}{c}\underline{\textsf{Exterior angle of a regular polygon}}\\\\\textsf{Exterior Angle} = (360^(\circ))/(n)\\\\\textsf{where $n$ is the number of sides}\end{array}}`

For a regular 20-gon, the value of n is 20.

Therefore, substitute n = 20 into the exterior angle formula:

`\begin{aligned}\textsf{Exterior Angle}&= (360^(\circ))/(20)\\\\&= 18^(\circ)\end{aligned}`

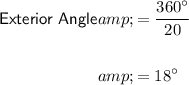
So, each exterior angle of a regular 20-gon measures 18°.