Question

Pls help asap. correct answers only.

Answer 1

`\textsf{1.}\quad (f \circ g)(x)=x^2-7x+12`

`\textsf{2.}\quad f^(-1)(x)=(x-3)^3+5`

`\textsf{3.}\quad \textsf{Yes, because $f(g(x))=x$ and $g(f(x))=x$.}`

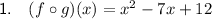
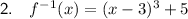
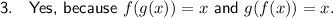
Explanation:

Question 1

Given functions:

`f(x)=x^2-x`

`g(x)=x-3`

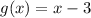
To find the composite function (f o g)(x), we can substitute the function g(x) in place of the x in function f(x). Therefore:

`\begin{aligned}(f \circ g)(x)&= f(g(x))\\&=f(x-3)\\&=(x-3)^2-(x-3)\\&=x^2-6x+9-x+3\\&=x^2-7x+12\end{aligned}`

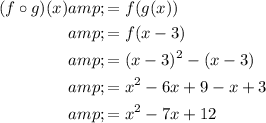
Therefore, (f o g)(x) is:

`\large\boxed{\boxed{(f \circ g)(x)=x^2-7x+12}}`

`\hrulefill`

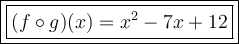
Question 2

Given function:

`f(x)=\sqrt[3]{x-5}+3`

To find the inverse of the given function, begin by swapping x and y:

`x=\sqrt[3]{y-5}+3`

Solve for y:

`\begin{aligned}x&=\sqrt[3]{y-5}+3\\x-3&=\sqrt[3]{y-5}\\(x-3)^3&=y-5\\(x-3)^3+5&=y\end{aligned}`

Therefore, the inverse of the given function is:

`\large\boxed{\boxed{f^(-1)(x)=(x-3)^3+5}}`

`\hrulefill`

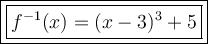
Question 3

Given functions:

`f(x)=-(1)/(3)x+5`

`g(x)=-3x+15`

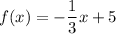
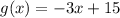
To determine if two functions are inverses of each other, we need to check if their composition results in the identity function:

`f(g(x)) = x`

`g(f(x)) = x`

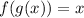
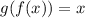
Find f(g(x)) by inputting function g(x) in place of the x in function f(x):

`\begin{aligned}f(g(x))&=f(-3x+15)\\\\&=-(1)/(3)(-3x+15)+5\\\\&=\left(-(1)/(3)\right)\cdot (-3x)+\left(-(1)/(3)\right)\cdot15+5\\\\&=x-5+5\\\\&=x\end{aligned}`

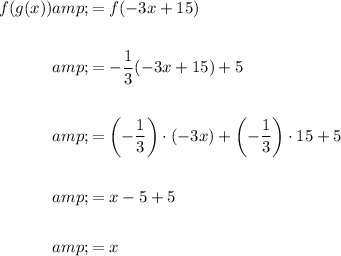
Find g(f(x)) by inputting function f(x) in place of the x in function g(x):

`\begin{aligned}g(f(x))&=g\left(-(1)/(3)x+5\right)\\\\&=-3\left(-(1)/(3)x+5\right)+15\\\\&=(-3)\cdot \left(-(1)/(3)x\right)+(-3)\cdot 5+15\\\\&=x-15+15\\\\&=x\end{aligned}`

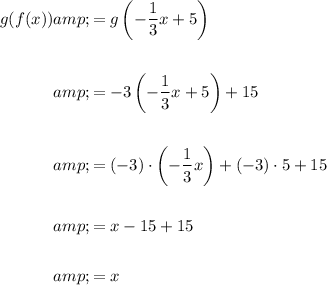
Since both f(g(x)) and g(f(x)) equal x, the functions f(x) and g(x) are inverses of each other.