Answer:
3x + 4
Explanation:
Given rational expression:
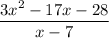

Method 1 - Long Division
To find the quotient of the given expression we can perform long division, as follows:
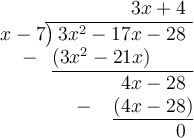
Therefore, the quotient is 3x + 4.

Method 2 - Synthetic Division
To find the quotient of the given expression we can perform synthetic division.
Place 7 in the division box, and write the coefficients of the dividend in descending order, then perform synthetic division:

The bottom row (except the last number) gives the coefficients of the quotient. The degree of the quotient is one less than that of the dividend. The last number in the bottom row is the remainder.
Therefore, the quotient of the given function is 3x - 4.

Method 3 - Factoring
To find the quotient of the given expression we can first factor the numerator 3x² - 17x - 28.
To factor a quadratic in the form ax² + bx + c, find two numbers that multiply to ac and sum to b.
In this case, a = 3, b = -17 and c = -28. Therefore, the product of a and c is:

The factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84.
Therefore, the two numbers that multiply to 84 and sum to -17 are 4 and -21.
Rewrite b as the sum of these two numbers:
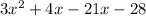
Factor the first two terms and the last two terms separately:

Factor out the common term (3x + 4):
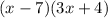
Therefore, the rational expression can be written as:
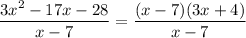
Cancel the common factor x - 7:

Therefore, the quotient of the given function is 3x - 4.