(G ° F)(-2) where G(x)=x^2 and F(x)=2x+3

Question

asked Oct 23, 2024 167k views

2 Answers

Mynd · Answer 1 · 2024-10-24T05:40:06+0000

The answer is -4x^3 + 6x^2

1. Multiply the polynomial (x^2)(2x + 3) which is 2x^3 - 3x^2
2. Multiply that by (-2) which gives us our answer :)

Veridian · Answer 2 · 2024-10-29T12:30:11+0000

Answer:

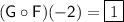
$\sf (G \circ F) (-2) = \boxed{1}$

Explanation:

To find:

$\sf (G \circ F) (-2) = ?$

Given:

$\sf G(x)=x^2$

$\sf F(x)=2x+3$

Solution:

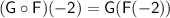
$\sf (G \circ F) (-2) = G(F(-2))$

In order to find
$\sf (G \circ F) (-2)$ , we first need to find the value of F(-2).

Then, we can substitute that value into G(x) to find the final answer.

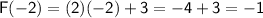
$\sf F(-2) = (2)(-2) + 3 = -4 + 3 = -1$

Now that we know F(-2) = -1, we can substitute that value into G(x) to find
$\sf (G \circ F) (-2)$ .

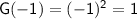
$\sf G(-1) = (-1)^2 = 1$

Therefore,
$\sf (G \circ F) (-2) = \boxed{\sf 1}$