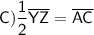Question

Given that points A, B, and C are the midpoints of their respective sides, which of the following is true about the figure?

Answer 1

`\textsf{C)}\quad (1)/(2)\overline{YZ}=\overline{AC}`

Explanation:

The Midline Theorem states that the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half its length.

Line segment AC connects the midpoints of sides YX and ZX. Therefore, line segment AC is parallel to side YZ and half its length.

`\overline{AC}=(1)/(2)\overline{YZ}`

Answer 2

`\sf C) (1)/(2)\overline{YZ}=\overline{AC}`

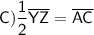
Explanation:

The midpoints of all triangles divide the mid-segment line which is half the base. This is a property of triangles known as the Mid-segment Theorem. It states that:

" A mid-segment of a triangle is parallel to the base of the triangle and is half the length of the base."

By this theorem, we can conclude that AC || YZ and AC = ½ YZ.

Therefore, the correct option is:

`\sf C) (1)/(2)\overline{YZ}=\overline{AC}`