Question

Use the given conditions to write an equation for the line in​ point-slope form and​ slope-intercept form. Passing through ​(4​,​-7) and perpendicular to the line whose equation is x+6y=11 Write an equation for this line in​ point-slope form.

Answer 1

Sure! To find the equation of a line perpendicular to the given line, we need to determine the slope of the given line and then find the negative reciprocal to get the slope of the perpendicular line.

The equation x + 6y = 11 can be rewritten in slope-intercept form as y = (-1/6)x + 11/6. The slope of this line is -1/6.

Since the perpendicular line has a negative reciprocal slope, the slope of the perpendicular line is 6.

Now we can use the point-slope form of a line to find the equation. Using the point (4, -7) and the slope 6, the equation in point-slope form is:

y - (-7) = 6(x - 4)

Simplifying this equation gives:

y + 7 = 6x - 24

So the equation of the line in point-slope form is y = 6x - 31.

Answer 2

↠ Answer:

y + 7 = 6(x - 4)

↠ Step-by-step explanation:

We're given the following conditions for a line's equation :

→ The line passes through (4,-7)

→ It's perpendicular to x + 6y = 11.

First, let's focus on the second condition. What does it tell us? The new line is perpendicular to x + 6y = 11. So their slopes are going to be opposite reciprocals; that happens with every single pair of perpendicular lines. But to find the slope of this line, we'll first have to write its equation in the form of slope-intercept. Slope-intercept is y = mx + b, where the parameter "m" defines the slope and the parameter "b" defines the y-intercept.

Our equation again :

→ x + 6y = 11

First, we need to subtract x from both sides :

→ 6y = 11 - x

→ 6y = -x + 11

It's starting to look like slope-intercept, but we still need to isolate y. And to do that, we need to divide both sides by 6 :

→
`\sf{y=-\cfrac{x}{6}+\cfrac{11}{6}}`

→
`\sf{y=-\cfrac{1}{6}x+\cfrac{11}{6}}`

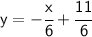
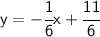
We now have our slope-intercept equation. Now, to find the slope, we'll look at the number in front of x. In this case it's -1/6. But it's not the slope of the new line; we still need to find the opposite reciprocal of -1/6.

`\textsl{Opposite reciprocal of -1/6 = 6}`

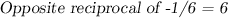
So, the new line's slope is 6.

To find its point-slope equation, we need to know the point; and we do. The point is (4,-7); so we plug it in :

→
`\underbrace{\boldsymbol{\sf{y-y_1=m(x-x_1)}}}_\sf{Point-slope}`

--

→
`\sf{y-(-7)=6(x-4)}`

→
`\sf{y+7=6(x-4)}`

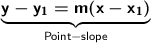
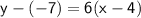
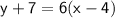
Therefore, the point-slope equation is y + 7 = 6(x - 4).