Question

A tank whose bottom is a mirror is field with water to a depth of 20cm a small object hange 8cm under the surface of water. What is the apparent depth of its image when viewed at normal incidence

Answer 1

The apparent depth of an object in water always appears to be shallower than its actual depth due to the refraction of light. When viewed at normal incidence, the apparent depth is equal to the actual depth, in this case, 8cm.

Step-by-step explanation:

The apparent depth of an object in water always appears to be shallower than its actual depth due to the refraction of light. When light passes from water to air, it bends away from the normal, causing the object's image to appear higher than its actual position. This phenomenon is known as apparent depth.

In the given scenario, the small object hanging 8cm under the surface of water will have an apparent depth equal to its actual depth because it is viewed at normal incidence. Normal incidence means that the light rays are travelling perpendicular to the surface, and in this case, there is no bending of light due to refraction.

Therefore, the apparent depth of the object's image will be 8cm.

Answer 2

6 cm

Step-by-step explanation:

When an object is submerged in a transparent medium, such as water, and viewed from outside the medium, it appears to be at a different depth than its actual position.

This is due to the bending of light as it passes from one medium (e.g., water) to another (e.g., air).

The apparent depth (d') of an object submerged in a liquid can be calculated using the following formula:

`d' = (d)/(n)`

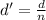
• d' is the apparent depth of the object.
• d is the actual depth of the object below the liquid's surface.
• n is the refractive index of the liquid.

The refractive index of water is approximately 1.333.

In this case, the actual depth of the object (d) is 8 cm below the water's surface, and the refractive index (n) of water is 1.333.

Now, we can calculate the apparent depth (d'):

`d' = (8 cm)/(1.333) = 6 cm`

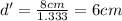
So, the apparent depth of the object when viewed at normal incidence is approximately 6 cm.