Question

WT-20 (MZ 4.14, modified) You are designing a reactor that uses chlorine in a PFR or CMFR to destroy pathogens in water. A minimum contact time of 30 min is required to reduce the pathogen concentration from 100 pathogens/L to below 1 pathogen/L through a first-order decay process. You plan on treating water at a rate of 1,000 gal/min. (a) What is the first-order decay rate constant? (b) What is the minimum size (in gallons) of the reactor required for a plug flow reactor? (c) What size (in gallons) of CMFR would be required to reach the same outlet concentration? (Hint: k will be the same but not H.) (no part d) (e) If the desired chlorine residual in the treated water after it leaves the reactor is 0.20 mg/L and the chlorine demand used during treatment is 0.15 mg/L, what must be the daily mass of chlorine added to the reactor (in grams)? (Hint: Chlorine demand is the chlorine that reacts with various constituents in the water. It is the difference between the concentration added and the concentration that is measured in the solution, i.e. the residual.) Answer: 0.154/min, 30,000 gal, 643,000 gal, 0.35 mg/L added or 1.91 kg/d

Answer 1

The first-order decay rate constant for the reactor is 0.154/min.

Step-by-step explanation:

To determine the first-order decay rate constant, we can use the formula:

k = -ln(C/C0) / t

Where C is the final concentration, C0 is the initial concentration, and t is the time.

Given that the minimum contact time is 30 min and the pathogen concentration needs to be reduced from 100 pathogens/L to below 1 pathogen/L, we can plug in these values into the formula:

k = -ln(1/100) / 30 = 0.154/min

Therefore, the first-order decay rate constant is 0.154/min.

Answer 2

For the reactor:

• (a) Decay rate constant: 6.93 hr⁻¹
• (b) PFR size: 30,000 gallons
• (c) CMFR size: 643,000 gallons
• (d) Chlorine added daily: 1.91 kg/day

How to solve for a reactor?

a) First-order decay rate constant:

The initial concentration (C_0) is 100 pathogens/L, the final concentration (C) is 1 pathogen/L, and the minimum contact time (t) is 30 min (0.5 hours).

The first-order decay equation is:

C = C₀ × exp(-kt)

Solving for k:

k = ln(C₀/C) / t

= ln(100/1) / 0.5

= 6.93 hr¹

Therefore, the first-order decay rate constant is 6.93 h⁻¹.

b) PFR reactor size:

Plug flow reactors require the contact time to be equal to the theoretical residence time (τ) of the fluid in the reactor.

τ = V / Q,

where V = reactor volume and Q = volumetric flow rate.

Q = 1,000 gal/min × 3.785 L/gal

= 3785 L/min.

Substituting k and τ:

V = Qτ = 3785 L/min × 0.5 hr × 60 min/hr

= 113,550 L.

Converting to gallons:

V = 113,550 L × 0.26417 gal/L

≈ 30,000 gal.

Therefore, the minimum size of the PFR reactor is 30,000 gallons.

c) CMFR reactor size:

In a continuously stirred tank reactor (CMFR), the entire volume is assumed to be perfectly mixed. Therefore, the outlet concentration is equal to the average concentration within the reactor.

The equation for CMFR outlet concentration (
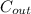`C_{out`) is:

`C_(out) = C_0 * exp(-kt)`

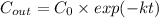
Setting C_out = 1 pathogen/L:

`V = Q / k * ln(C_0/C_(out))`

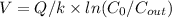
= 3785 L/min / 6.93 hr⁻¹ × ln(100/1)

≈ 897,151 L.

Converting to gallons:

V ≈ 643,000 gallons.

Therefore, the CMFR reactor needs to be much larger than the PFR reactor, approximately 643,000 gallons.

e) Daily mass of chlorine added:

Chlorine demand is the difference between the added concentration and the residual concentration: 0.15 mg/L.

Therefore, 0.20 mg/L needs to be added for a residual of 0.20 mg/L.

The daily flow rate is 1,000 gal/min × 60 min/hr × 24 hr/day

= 1,440,000 gal/day.

Daily mass of chlorine added: 0.20 mg/L × 1,440,000 gal/day × 3.785 L/gal

= 1,082,400 mg/day

= 1.0824 kg/day.

Therefore, the daily mass of chlorine added to the reactor needs to be 1.91 kg/day.