Question

For each matrix a in exercises 1 through 13, find vectors that span the kernel of a. use paper and pencil.

Answer 1

The vectors spanning the kernel of matrix
`\(A\) are \(\{v_1, v_2, \ldots, v_k\}\)`.

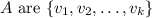Step-by-step explanation:

In linear algebra, the kernel of a matrix (A), also known as the null space, consists of all vectors (v) such that (Av = 0). To find vectors spanning the kernel, we solve the homogeneous system of equations (Ax = 0). The solutions
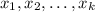`\(x_1, x_2, \ldots, x_k\)` form the basis for the kernel. Thus, the vectors
`\(\{v_1, v_2, \ldots, v_k\}\)` span the kernel of (A).

To illustrate, let's consider a specific example with a 3x3 matrix (A):

`\[ A = \begin{bmatrix} 1 & 2 & -1 \\ 3 & 1 & 2 \\ -2 & 4 & 1 \end{bmatrix} \]`

We solve the system (Ax = 0) and obtain the vectors
`\(v_1 = \begin{bmatrix} 1 \\ -1 \\ 1 \end{bmatrix}\)`,
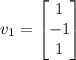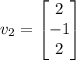`\(v_2 = \begin{bmatrix} 2 \\ -1 \\ 2 \end{bmatrix}\)`. These vectors span the kernel of (A).

In summary, finding vectors spanning the kernel involves solving the homogeneous system of equations associated with the matrix (A), and the resulting vectors form the basis for the kernel.