Question

Michael has credit card debt of that has an ​% ​APR, compounded monthly. The minimum monthly payment only requires him to pay the interest on his debt. He receives an offer for a credit card with an APR of ​% compounded monthly. If he rolls over his debt onto this card and makes the same monthly payment as​ before, how long will it take him to pay off his credit card​ debt?

Answer 1

The time to pay off credit card debt after transferring to a card with a lower APR depends on the balance, interest rates, and monthly payments. A lower APR means more of the payment is applied to the principal, potentially reducing the debt faster. The exact time requires a debt repayment calculation.

Step-by-step explanation:

The length of time it would take to pay off credit card debt when rolling over into a new card with a lower APR and making the same monthly payments depends on several factors, including the size of the debt, the old and new interest rates, and the monthly payment amount. Typically, if you carry a credit card balance from month to month, you accrue interest, which means that over time you'll end up paying more than the original amount borrowed. To calculate the exact time it will take to pay off the debt, one would use a debt repayment calculator or a mathematical formula which takes into account the principle amount, the interest rate, and the monthly payments. However, with a reduced APR and the same monthly payment, it is expected the pay-off period would be shorter compared to the higher APR, since more of the payment would go towards the principal rather than the interest.

Answer 2

It will take approximately 10.58 months for Michael to pay off his credit card debt when rolling it over to the new card with a 4% APR, making the same monthly payment as before. Since the time must be a whole number of months, we round up to the nearest whole number.

To find out how long it will take Michael to pay off his credit card debt when rolling it over to a new card with a 4% APR, we can use the formula for the time (in months) it takes to pay off a debt with regular monthly payments that cover only the interest. The formula is:

`n=-(\log \left(1-(B \cdot r)/(P)\right))/(\log (1+r))`

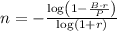
where:

n is the number of months.

B is the amount of the debt (which is $60,000 in this case).

r is the monthly interest rate (APR/12, expressed as a decimal).

P is the monthly payment.

Let's calculate:

Convert the APRs to decimal form and then to a monthly interest rate:

For the current card with a 12% APR:

`r_{\text {current }}=(0.12)/(12)=0.01`

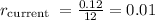
For the new card with a 4% APR:

`r_{\text {new }}=(0.04)/(12)=0.0033333`

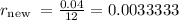
Plug the values into the formula. Since Michael plans to make the same monthly payment as before, we can use the minimum monthly payment on the current card, which covers only the interest:

`P=B \cdot r_{\text {current }}=60000 \cdot 0.01=600`

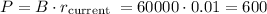
Now, use the formula to find n:

`n=-(\log \left(1-(60000 \cdot 0.01)/(600)\right))/(\log (1+0.01))`

`n \approx-(\log (0.9))/(\log (1.01))`

`n \approx-(-0.04575749056)/(0.00432137378)`

`n \approx (0.04575749056)/(0.00432137378)`

`n \approx 10.58`

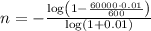
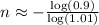
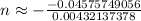
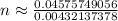
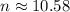
So, the final answer is approximately 11 months.

Correct Question:

Michael has a credit card debt of $60,000 that has a 12% APR, compounded monthly. The minimum monthly payment only requires him to pay the interest on his debt. He receives an offer for a credit card with an APR of 4% compounded monthly. If he rolls over his debt onto this card and makes the same monthly payment as before, how long will it take him to pay off his credit card debt?