The inlet area of the diffuser is approximately
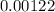 .
.
To determine the inlet area of the diffuser, we can use the mass flow rate equation for a compressible fluid in a steady-flow process. The mass flow rate
 can be expressed as:
can be expressed as:
![\[ \dot{m} = \rho A V \]](https://img.qammunity.org/2024/formulas/physics/high-school/r5m4yal3m92hdt507bhtncdycwnjk8imfh.png)
where:
 is the mass flow rate (1.2 kg/s),
is the mass flow rate (1.2 kg/s),
 is the density of the fluid,
is the density of the fluid,
 is the cross-sectional area, and
is the cross-sectional area, and
V \is the velocity of the fluid.
To find the density
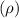 , you can use the ideal gas law for the given conditions. The ideal gas law is given by:
, you can use the ideal gas law for the given conditions. The ideal gas law is given by:
![\[ PV = mRT \]](https://img.qammunity.org/2024/formulas/physics/high-school/hxk4c2tfwjo2xrwb7117rc499lyqvb2ird.png)
where:
P is the pressure (0.5 MPa),
V is the specific volume (inverse of density),
m is the mass (1.2 kg),
R is the specific gas constant for refrigerant 134a, and
T is the temperature (50°C).
Let's convert the pressure to Pascals and the temperature to Kelvin and then use the ideal gas law to find the density:
![\[ P = 0.5 \, \text{MPa} = 500,000 \, \text{Pa} \]](https://img.qammunity.org/2024/formulas/physics/high-school/gich83pobcinytge81zumbaojcagqne607.png)
![\[ T = 50 + 273.15 \, \text{K} = 323.15 \, \text{K} \]](https://img.qammunity.org/2024/formulas/physics/high-school/s87h72pzs04lt839fjkk06inz8j95ls0wp.png)
Now, rearrange the ideal gas law to solve for density
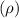 :
:
![\[ \rho = (m)/(V) = (P)/(RT) \]](https://img.qammunity.org/2024/formulas/physics/high-school/cznwv757mucbhmu7fw7p6ioqh6k0f95a5m.png)
Once you have the density, you can rearrange the mass flow rate equation to solve for the cross-sectional area (\( A \)):
![\[ A = \frac{\dot{m}}{\rho V} \]](https://img.qammunity.org/2024/formulas/physics/high-school/a9ms01sxmaiu5yodafb8eba3lplgvd9ojx.png)
Firstly, let's calculate the density
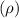 using the ideal gas law:
using the ideal gas law:
![\[ \rho = (P)/(RT) \]](https://img.qammunity.org/2024/formulas/physics/high-school/89zp7ovfxf4lwmifxgda9p4dciakvelq5t.png)
where:
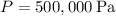 (pressure in Pascals),
(pressure in Pascals),
R is the specific gas constant for refrigerant 134a, and
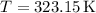 (temperature in Kelvin).
(temperature in Kelvin).
The specific gas constant ( R ) for refrigerant 134a is approximately 188.92 J/(kg·K).
![\[ \rho = \frac{500,000 \, \text{Pa}}{188.92 \, \text{J/(kg·K)} * 323.15 \, \text{K}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/y2kbo6vgf1zyh5j0orp5swer5pj377cy11.png)
Now, calculate
 . The result will be in kg/m³.
. The result will be in kg/m³.
![\[ \rho \approx (500,000)/(61,088.238) \, \text{kg/m³} \approx 8.18 \, \text{kg/m³} \]](https://img.qammunity.org/2024/formulas/physics/high-school/eqophe08akb53szzo5ma80e498gfn7x3at.png)
Now, use the mass flow rate equation to find the cross-sectional area
 :
:
![\[ A = \frac{\dot{m}}{\rho V} \]](https://img.qammunity.org/2024/formulas/physics/high-school/a9ms01sxmaiu5yodafb8eba3lplgvd9ojx.png)
where:
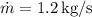 (mass flow rate),
(mass flow rate),
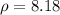 (density), and
(density), and
 (velocity).
(velocity).
![\[ A = (1.2)/(8.18 * 120) \]](https://img.qammunity.org/2024/formulas/physics/high-school/ersqiethu5tdvcdt4r6nvj3uud0853yba2.png)
Now, calculate A .
![\[ A \approx (1.2)/(981.6) \, \text{m²} \approx 0.00122 \, \text{m²} \]](https://img.qammunity.org/2024/formulas/physics/high-school/9h04vyjtcn4zme0kry46c1bygfp3tddx6m.png)
Therefore, the inlet area of the diffuser is approximately
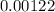 .
.