Question

In this puzzle, the object is to fill a

3 x 3 square with the nine numbers
from 0 through 8 (using each of
them exactly once) in such a way
that the numbers in the first, second,
and third rows will add up to three
numbers in the proportion 1:2:3.
Simultaneously, the same proportion
has to be achieved for the first,
second, and third columns.

Answer 1

`\begin{array}{ccc}0&1&5\\2&3&7\\4&8&6\end{array}\qquad\begin{array}{ccc}1&0&5\\2&4&6\\3&8&7\end{array}\qquad\begin{array}{ccc}2&0&4\\1&5&6\\3&7&8\end{array}`

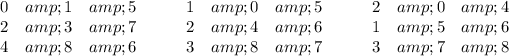
Explanation:

You want a 3×3 square consisting of the digits 0–8 such that the rows in order have sums in the ratio 1:2:3, and the columns in order have the same sums.

Sums

The digits 0-8 have the sum 8·9/2 = 36. For the rows or columns to have the required ratios, their sums must be 6, 12, 18.

The only ways to make sums of 6 from the given digits are ...

0 +1 +5 = 0 +2 +4 = 1 +2 +3

The only ways to make sums of 18 from the given digits are ...

3 +7 +8 = 4 +6 +8 = 5 +6 +7

Arrangements

There are only 6 ways to choose one of the 6-sums and one of the 18-sums such that all the digits are different. Those 6 ways give rise to 6 solutions to the problem.

Each solution has a transpose (interchanged rows and columns) that is also a solution. So, there are only 3 unique solutions to the puzzle.

The solutions are listed in the Answer section, above.

<95141404393>