To find the general form of the equation of the line with the given intercepts
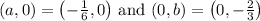 , we'll start with the intercept form:
, we'll start with the intercept form:
![\[(x)/(a) + (y)/(b) = 1\]](https://img.qammunity.org/2024/formulas/mathematics/college/5c1qeb2p40yrdlgwx3we9piumw4qkl4qef.png)
Substituting the given values
 , we get:
, we get:
![\[-(x)/((1)/(6)) - (y)/((2)/(3)) = 1\]](https://img.qammunity.org/2024/formulas/mathematics/college/biymakcdcwwm4jostzxaycgwepdjawbt82.png)
To eliminate the fractions, we'll multiply both sides of the equation by
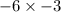 :
:
![\[(-6 * -3) * (x)/(-1/6) + (-6 * -3) * (y)/(-2/3) = (-6 * -3) * 1\]](https://img.qammunity.org/2024/formulas/mathematics/college/hsv2vgzctjj9khtfpxci3qii2euu01ujkl.png)
Simplifying, we get:
![\[-2x - 9y = -18\]](https://img.qammunity.org/2024/formulas/mathematics/college/nv7gpei76sl0lqpb315j2ha2cpyq3ateu1.png)
This is the general form
 of the line, with
of the line, with
 .
.