Question

Rain is falling vertically with a Speed of 35 m s^-1 . Wind starts blowing after sometimes with a speed of 12 m s^1 in east to west direction. In which direction should a student waiting at the bus stop hold their umbrella?

​

Answer 1

18.9° with the vertical (northeast direction)

Step-by-step explanation:

To determine the direction in which the student should hold their umbrella, we need to consider the vectors of rain and wind. The student should align the umbrella so that it opposes the net effect of these vectors.

Draw a diagram (attached) showing the following information:

• The rain is falling vertically with a speed of 35 ms⁻¹, so its velocity vector is <0, -35> (assuming upward is positive).
• The wind is blowing from east to west with a speed of 12 ms⁻¹, which is in the negative x-direction.

To find the measure of angle θ, we can use the tangent ratio:

`\tan\theta =\sf (opposite\;side)/(adjacent\;side)`

`\tan\theta = (12)/(35)`

`\theta = \tan^(-1)\left((12)/(35)\right)`

`\theta=18.9246444...^(\circ)`

`\theta=18.9^(\circ)\; \sf(nearest\;tenth)`

So, the student should hold their umbrella at an angle of approximately 18.9° with the vertical to counteract both the rain and the wind. This angle indicates that they should hold the umbrella in the northeast direction.

Answer 2

vertically and slightly to the east about 18.92°

Step-by-step explanation:

Given:

• Rain is falling vertically with a speed of 35 m s^-1.
• Wind starts blowing after sometimes with a speed of 12 m s^1 in east to west direction.

To find:

• Direction of a student

Solution:

To find the direction in which the student should hold their umbrella, we need to find the relative velocity of the raindrops.

The relative velocity of the raindrops is given by:

`\sf v_r = \sqrt{v_x^2+ v_y^2`

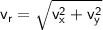
where:

• vr is the relative velocity of the raindrops
• vx is the horizontal velocity of the raindrops (which is 0 m
• s^-1 since they are falling vertically
• vy is the vertical velocity of the raindrops (which is 35 m s^-1)

Therefore, the relative velocity of the raindrops is:

`\sf v_r = √(0^2 + 35^2) = 35 m s^(-1)`

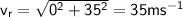
The direction of the relative velocity is given by:

`\sf \theta = tan^(-1)\left( (v_y )/( v_x)\right)`

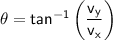
where:

• θ is the direction of the relative velocity
• vy is the vertical velocity of the raindrops (which is 35 m s^-1)
• vx is the horizontal velocity of the raindrops (which is 0 m s^-1 since they are falling vertically)

Therefore, the direction of the relative velocity of the raindrops is:

`\sf \theta = tan^(-1) \left((35 )/( 0)\right) = 90^\circ`

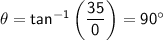
This means that the raindrops are falling vertically.

To protect themselves from the rain, the student should hold their umbrella vertically.

However, the wind is also blowing in an east to west direction.

This means that the student will need to tilt their umbrella slightly to the east to protect themselves from the rain.

The angle at which the student should tilt their umbrella is given by:

`\sf \theta = tan^(-1)\left((v_(wind ))/(v_(rain))\right)`

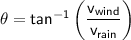
where:

• θ is the angle at which the student should tilt their umbrella
• v wind is the speed of the wind (which is 12 m s^-1)
• v rain is the speed of the raindrops (which is 35 m s^-1)

Therefore, the angle at which the student should tilt their umbrella is:

`\sf \theta = tan^(-1)\left((12)/(35)\right)\approx 18.92^\circ`

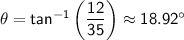
Therefore, the student should hold their umbrella vertically and tilt it slightly to the east by an angle of 18.92° to protect themselves from the rain.

Answer:

The student should hold their umbrella vertically and tilt it slightly to the east by an angle of 18.9 ° to protect themselves from the rain.