Use the Change of Base Formula to show that log3(x) = ln(x)/ln(3) is equal

Question

asked Oct 22, 2024 217k views

2 Answers

Yoichi · Answer 1 · 2024-10-24T06:16:55+0000

Answer:

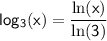
$\sf log_3(x) = (\ln(x))/(\ln(3))$

Explanation:

The change of base formula states that for any positive base a and positive number x ,

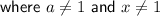
$\sf \textsf{where $a \\eq 1$ and $x \\eq 1$}$

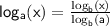
$\sf log_a(x) = (\log_b(x))/(\log_b(a))$

To show that:

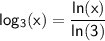$\sf log_3(x) =( ln(x))/(ln(3))$ , we can use the change of base formula with base b = e, where e is the natural base.

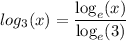
$\sd log_3(x) = (\log_e(x))/(\log_e(3))$

But

$\textsf{$\log_e(x) = \ln(x)$ and $\log_e(3) = \ln(3)$}$

so we have:

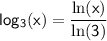
$\sf log_3(x) = (\ln(x))/(\ln(3))$

Therefore, we have shown that
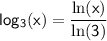$\sf log_3(x) = (\ln(x))/(\ln(3))$ is equal.

Another way to show this equality:

log3(x) is the power to which 3 must be raised to get x.

ln(x) is the power to which e must be raised to get x.

Therefore,

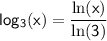
$\sf log_3(x) = (\ln(x))/(\ln(3))$

`

DrOnline · Answer 2 · 2024-10-27T05:22:32+0000

Answer:

$\log_3(x) = (\ln(x))/(\ln(3))$

Explanation:

To express a logarithm in one base as the ratio of logarithms in another base, we can use the change of base formula:

$\boxed{\begin{array}{b}\underline{\textsf{Change of base}}\\\\\log_b(a) = (\log_c(a))/(\log_c(b))\end{array}}$

We want to express log₃(x) in terms of natural logarithms (ln).

$\textsf{Since\;$\ln(x)=\log_e(x)$,\;then:}$

Substitute these values into the change of base formula:

$\log_3(x) = (\log_e(x))/(\log_e(3))$

Since
$\log_e$ is simply the natural logarithm (ln), we can rewrite this as:

$\log_3(x) = (\ln(x))/(\ln(3))$

So, log base 3 of x is equal to ln(x) divided by ln(3), as shown using the change of base formula.