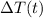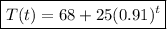Question

A cup of coffee is initially at a temperature of 93°F . The difference between its temperature in the room room temperature of 68°F decreases by 9% each minute . Write a function describing the temperature of the coffee as a function of time?

Answer 1

`T(t) = 68\°F + 25(0.91)^t`

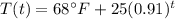
Explanation:

The general formula for relative (exponential) decay is:

`f(t) = a(1 - r)^t`

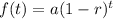
where
`a` is the initial value,
`r` is the rate of decay,
`t` is the time passed since a defined point
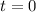`t=0` (in this case, when the coffee is 93°F), and
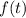`f(t)` is the value of the function at a specified input
`t`.

In this case, the initial temperature difference (a) is the difference between the coffee's initial temperature and the room temperature, which is:

93°F - 68°F = 25°F

The given rate of decay (r) is 9%, or 0.09 when expressed as a decimal.

So, the temperature difference between the coffee and the room as a function of time is modeled by the equation:

`\Delta T(t) = 25(1 - 0.09)^t`

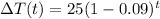
which simplifies to:

`\Delta T(t) = 25(0.91)^t`

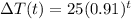
To get the actual temperature of the coffee, we need to add this to the room temperature (68°F):

`T(t) = 68 + \Delta T(t)`

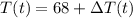
↓ plugging in the expression for
`\Delta T(t)`

`\boxed{T(t) = 68 + 25(0.91)^t}`