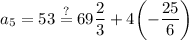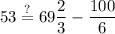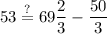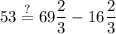Question

The sum of the first 15 terms of an arithmetic series is 615.

Given that the fifth term is 53, find the common difference.

Answer 1

`d = -(25)/(6)`

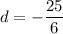
Explanation:

The following formulas model an arithmetic sequence:

`a_n = a_1 + d(n-1)`

`S_n = n\!\left((a_1 + a_n)/(2)\right)`

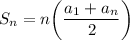
where
`a_1` is the first term of the sequence and
`d` is the common difference between two consecutive terms.

We are given the following information:

`a_5 = 53 = a_1 + d(5-1)`

`S_(15) = 615 = (15)/(2)(2a_1 + d(15-1))`

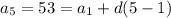
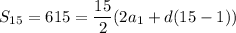
Now, we have a system of equations with the variables
`a_1` and
`d`. We can solve for them using substitution.

`53 = a_1 + 4d`

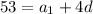
↓ subtracting
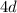`4d` from both sides to isolate
`a_1`

`a_1 = 53 - 4d`

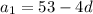
↓ substituting this definition for
`a_1` in terms of
`d` into the other equation

`615 = (15)/(2)(2[53 - 4d] + 14d)`

↓ multiplying both sides by 2/15

`82 = 2[53-4d] + 14d`

↓ expanding the right side using the distributive property

`82 = 106 - 8d + 14d`

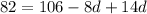
↓ combining like terms

`82 = 106 + 6d`

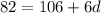
↓ subtracting 106 from both sides

`6d = -25`

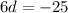
↓ dividing both sides by 6

`\boxed{d = -(25)/(6)}`

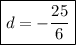
Further Note

We can plug this back into the definition for
`a_1` to solve for the first term:

`a_1 = 53 - 4\!\left(-(25)/(6)\right)`

`a_1 = 69(2)/(3)`

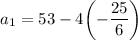
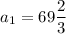
And we can check if this works for the fifth term by plugging this and the common difference back into that term's definition:

`a_5 = 53 \stackrel{?}{=} 69(2)/(3) + 4\!\left(-(25)/(6)\right)`

`53 \stackrel{?}{=} 69(2)/(3) - (100)/(6)`

`53 \stackrel{?}{=} 69(2)/(3) - (50)/(3)`

`53 \stackrel{?}{=} 69(2)/(3) - 16(2)/(3)`

`53\stackrel{\checkmark}{=} 53`