Question

Find the volume of the given solid. bounded by the coordinate planes and the plane 7x 4y z = 28

Answer 1

The volume of the solid bounded by the coordinate planes and the plane 7x + 4y + z = 28 is 224 cubic units.

Step-by-step explanation:

To find the volume of the solid bounded by the coordinate planes and the plane 7x + 4y + z = 28, we need to determine the region enclosed by this plane and the coordinate axes. This region forms a tetrahedron. The equation of the plane can be expressed in the form
`\(z = f(x, y)\)` by rearranging it. In this case,
`\(z = 28 - 7x - 4y\)`.

To find the limits of integration for x and y, we set z = 0 to find where the plane intersects the coordinate axes. Solving 28 - 7x - 4y = 0 for x and y, we get x = 4 and y = 7. Thus, the limits of integration for x are [0, 4] and for y, [0, 7]. The limits for z are [0, 28 - 7x - 4y].

Now, we set up the triple integral to find the volume:
`\[V = \int_0^4 \int_0^7 \int_0^(28 - 7x - 4y) dz \, dy \, dx\]`. Evaluating this triple integral gives V = 224 cubic units, which is the final answer representing the volume of the bounded solid. Understanding how to set up and evaluate triple integrals is crucial in calculating volumes of solids in three-dimensional space, making it an essential skill in calculus and applied mathematics.

Answer 2

The volume of the solid bounded by the coordinate planes and the plane
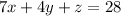`\(7x + 4y + z = 28\)` is 392 cubic units.

To find the volume of the solid bounded by the coordinate planes and the plane
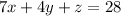`\(7x + 4y + z = 28\)`, we'll first identify the region enclosed by this plane and the coordinate axes.

The equation
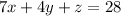`\(7x + 4y + z = 28\)` intersects the coordinate axes at points where x, y, or z is zero.

Setting (x = 0) gives us 4y + z = 28 or z = 28 - 4y.

Setting (y = 0) gives us 7x + z = 28 or z = 28 - 7x\).

Setting (z = 0) gives us 7x + 4y = 28.

In the x-y-z coordinate space you can visualize the region they enclose.

1. (z = 28 - 4y): This is a plane that intersects the z-axis at z = 28 and the y-axis at y = 7.

2. (z = 28 - 7x): This is a plane that intersects the z-axis at z = 28 and the x-axis at x = 4.

3. (7x + 4y = 28): This is a line that intersects the x-axis at x = 4 and the y-axis at y = 7.

The solid enclosed by these planes and the coordinate axes forms a triangular prism. To find its volume, we'll first find the area of the triangular base and then multiply it by the height.

The triangular base is formed by the intersection of the planes 7x + 4y = 28 and the coordinate axes, which happens at the points (4, 0, 0), (0, 7, 0), and (0, 0, 28).

The base's area can be found using the formula for the area of a triangle formed by three points in 3D space:

`\[ \text{Area of triangular base} = (1)/(2) * \text{base} * \text{height} \]`

`\[ \text{Area of triangular base} = (1)/(2) * 4 * 7 = 14 \]`

The height of the prism is the distance between the planes (z = 0) and (z = 28), which is 28.

Now, find the volume of the solid:

`\[ \text{Volume} = \text{Area of triangular base} * \text{height} \]`

`\[ \text{Volume} = 14 * 28 = 392 \]`

Therefore, the required volume is 392 cubic units.

Complete Question:

Find the volume of the given solid. bounded by the coordinate planes and the plane 7x + 4y + z = 28.