Question

You deposit 100,000 in an account that earns 6% per year, compounded annually. If you

withdraw one half of the annual interest at the end of each year, what will be the balance in the account at the end of 3 years?
(a) 109550.8 (b) 109272.7 (c) 9550.8 (d) 9272.7

Answer 1

(b) 109272.7.

Explanation:

1. Calculate the interest earned for the year.

2. Subtract half of the interest from the total interest earned to determine how much interest is added to the account.

3. Add the interest from step 2 to the principal to get the new balance for the year.

Repeat these steps for each of the 3 years.

Year 1:

1. Interest for Year 1 =
`\(100,000 * 0.06 = 6,000\)`.

2. Half of the interest =
`\(6,000/2 = 3,000\)`.

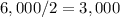Interest added to the account =
`\(6,000 - 3,000 = 3,000\)`.

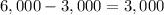3. New balance at the end of Year 1 =
`\(100,000 + 3,000 = 103,000\)`.

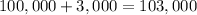Year 2:

1. Interest for Year 2 =
`\(103,000 * 0.06 = 6,180\)`.

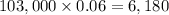2. Half of the interest =
`\(6,180/2 = 3,090\)`.

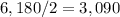Interest added to the account =
`\(6,180 - 3,090 = 3,090\)`.

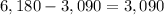3. New balance at the end of Year 2 =
`\(103,000 + 3,090 = 106,090\)`.

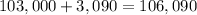Year 3:

1. Interest for Year 3 =
`\(106,090 * 0.06 = 6,365.4\)`.

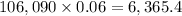2. Half of the interest =
`\(6,365.4/2 = 3,182.7\)`.

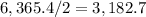Interest added to the account =
`\(6,365.4 - 3,182.7 = 3,182.7\)`.

3. New balance at the end of Year 3 =
`\(106,090 + 3,182.7 = 109,272.7\)`.

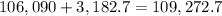The balance in the account at the end of 3 years will be
`\(109,272.7\)`.

So the correct answer is (b) 109272.7.