Question

How do you make 14x=10x-18x+x^(2) as standard form in quadratic equation??

Answer 1

`\[ x^2 - 22x = 0 \]`

Explanation:

To express the equation
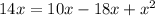`\( 14x = 10x - 18x + x^2 \)` in standard form for a quadratic equation, you need to rearrange terms and set the equation equal to zero. The standard form of a quadratic equation is:

`\[ ax^2 + bx + c = 0 \]`

1. Combine like terms:

- Combine all the
`\( x \)` terms on the right side:

`\( 10x - 18x = -8x \)`

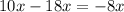
Using this, the equation becomes:

`\( 14x = x^2 - 8x \)`

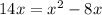
2. Move all terms to one side:

Subtracting
`\( 14x \)` from each side, we get:

`\( 0 = x^2 - 8x - 14x \)`

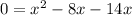
Combining the
`\( x \)` terms on the right:

`\( 0 = x^2 - 22x \)`

3. Re-arrange the equation to match the standard form:

`\( x^2 - 22x = 0 \)`

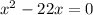
So, the equation in standard form is:

`\[ x^2 - 22x = 0 \]`