Answer:

Explanation:
The diagram shows a triangle with two of its sides measuring 12 cm and 5 cm. An altitude is drawn from the vertex between these sides, perpendicular to the opposite side, forming two smaller right triangles. One of these right triangles has legs of x cm and 3 cm, with a hypotenuse measuring 12 cm.
To find the value of x, we can use Pythagoras Theorem.

From observation of the triangle:
Substitute the values of a, b and c into the formula and solve for x:
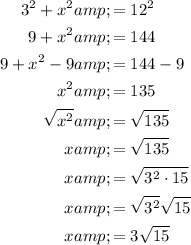
Therefore, the exact value of x is 3√(15) cm, which is approximately 11.6 cm (rounded to the nearest tenth).