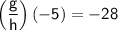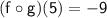Question

Precalc question
please show work!!

Answer 1

`\sf (f + g)(-2) = 6 + 4 = 10`

`\sf \left((g)/(h)\right)(-5) = -28`

`\sf (f \circ g)(5) = -9`

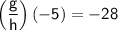
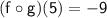
Explanation:

Given:

`\sf f(x) = -3x`

`\sf g(x) = |x-2|`

`\sf h(x) = (1)/(x+1)`

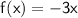
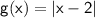
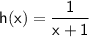
To find:

`\sf a) (f+g)(-2)`

`\sf b) \left((g)/(h)\right)`

`\sf c) (f\circ g)(5)`

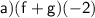
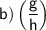
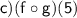
Solution:

Let's calculate each of the requested expressions step by step:

`\sf a) (f + g)(-2):`

`\sf (f + g)(-2) = f(-2) + g(-2)`

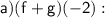
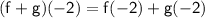
Now, plug in the values for f(x) and g(x):

`\sf f(-2) = -3(-2) = 6`

`\sf g(-2) = |(-2) - 2| = |(-4)| = 4`

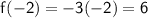
So,

`\sf (f + g)(-2) = 6 + 4 = 10`

`\sf b) \left((g)/(h)\right)(-5)`

`\sf \left((g)/(h)\right)(x) = (g(x))/(h(x))`

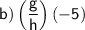
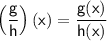
Now, plug in the values for g(x)and h(x):

`\sf g(x) = |x - 2|`

`\sf h(x) = (1)/(x + 1)`

So,

`\sf \left((g)/(h)\right)(x) = (|x - 2|)/((1)/(x + 1))`

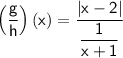
Now, multiply the numerator by the reciprocal of the denominator:

`\sf \left((g)/(h)\right)(x) = |x - 2| \cdot (x + 1)`

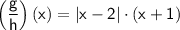
Now,

Substitute -5 in place of x.

`\sf \left((g)/(h)\right)(-5) = |-5 - 2| \cdot (-5+ 1)= 7\cdot -4 = -28`

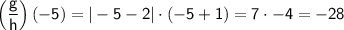
Now,

c)

`\sf (f \circ g)(5)`

`\sf (f \circ g)(5) = f(g(5))`

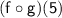
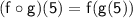
First, find g(5):

g(5) = |5 - 2| = |3| = 3

Now, plug in g(5) into f(x):

`\sf f(g(5)) = f(3) = -3 \cdot 3 = -9`

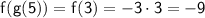
So,

`\sf (f \circ g)(5) = -9`

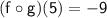
To summarize:

`\sf (f + g)(-2) = 6 + 4 = 10`

`\sf \left((g)/(h)\right)(-5) = -28`

`\sf (f \circ g)(5) = -9`

Answer 2

(a) (f + g)(-2) = 10

(b) (g/h)(-5) = -28

(c) (f o g)(5) = -9

Explanation:

Given functions:

`f(x)=-3x`

`g(x)=|x-2|`

`h(x)=(1)/(x+1)`

Part (a)

To find the value of (f + g)(-2), we need to add the values of the functions f(x) and g(x) at x = -2.

`\begin{aligned}(f+g)(x)&=f(x)+g(x)\\\\\implies (f+g)(-2)&=f(-2)+g(-2)\\&=-3(-2)+|-2-2|\\&=6+|-4|\\&=6+4\\&=10\end{aligned}`

Part (b)

To find the value of (g/h)(-5), we need to divide the values of the functions g(x) and h(x) at x = -5.

`\begin{aligned}\left((g)/(h)\right)(x)&=(g(x))/(h(x))\\\\\implies \left((g)/(h)\right)(-5)&=(g(-5))/(h(-5))\\\\&=(|-5-2|)/((1)/(-5+1))\\\\&=(|-7|)/((1)/(-4))\\\\&=(7)/(-(1)/(4))\\\\&=7 \cdot (-4)\\\\&=-28\end{aligned}`

Part (c)

To find the value of (f o g)(5), we need to first evaluate g(5) and then use that result as the input for the function f.

Evaluate g(5) by substituting x = 5 into function g:

`\begin{aligned}g(5)&=|5-2|\\&=|3|\\&=3\end{aligned}`

Now input the value of g(5) into function f:

`\begin{aligned}f(3)&=-3(3)\\&=-9\end{aligned}`

As one calculation:

`\begin{aligned}(f \circ g)(x)&=f(g(x))\\\\\implies (f \circ g)(5)&=f(g(5))\\&=f(|5-2|)\\&=f(|3|)\\&=f(3)\\&=-3\cdot 3\\&=-9\end{aligned}`