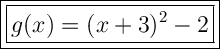Answer:
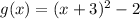
Explanation:
The vertex of an upward-opening parabola is the point at which the parabolic curve reaches its minimum value on the graph, and is the point where the curve changes direction.
From inspection of the given graph:
- Vertex = (-3, -2)
- y-intercept = (0, 7)
The vertex form of a quadratic equation is:
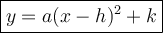
where:
- (h, k) is the vertex.
- a is the leading coefficient.
Substitute the vertex into the formula:
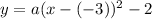

To find the leading coefficient (a), substitute the y-intercept (0, 7) into the equation:


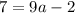
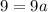


Therefore, the equation of g(x) in vertex form is: