Question

A particle moves along a line with a velocity v(t)=4t−6, measured in meters per second. Find the total distance the particle travels over the time interval [0,3] .

Answer 1

The total distance the particle travels over the time interval
`\([0,3]\) is \(9\)` meters.

Step-by-step explanation:

To find the total distance traveled by the particle, we need to integrate the absolute value of the velocity function over the given time interval.

The velocity function is given as
`\(v(t) = 4t - 6\).`To find the total distance traveled, integrate the absolute value of this function from \
`(t = 0\) to \(t = 3\):`

`\[ \text{Total distance} = \int_(0)^(3) |4t - 6| \, dt \]`

The absolute value function changes its sign when
`\((4t - 6) = 0\),` which gives
`\(t = (3)/(2)\).` So, we need to split the integral into two parts:

`\[ \text{Total distance} = \int_(0)^{(3)/(2)} (6 - 4t) \, dt + \int_{(3)/(2)}^(3) (4t - 6) \, dt \]`

Now, calculate each part separately:

`\[ \text{Total distance} = \left[6t - 2t^2\right]_(0)^{(3)/(2)} + \left[2t^2 - 6t\right]_{(3)/(2)}^(3) \]`

`\[ = (6 \cdot (3)/(2) - 2 \cdot ((3)/(2))^2) + (2 \cdot 3^2 - 6 \cdot 3) \]`

`\[ = (9 - (9)/(2)) + (18 - 18) \]`

`\[ = (9)/(2) \]`

`\[ = 9 \, \text{meters} \]`

Therefore, the total distance the particle travels over the time interval
`\([0,3]\) is \(9\)` meters.

Answer 2

The total distance the particle travels over the time interval
`\([0,3]\) is \(9\) meters.`

To find the total distance a particle travels over a time interval, we need to integrate the absolute value of the velocity function over that interval. This is because distance is a scalar quantity and does not depend on the direction of motion, whereas displacement is a vector quantity and does depend on direction.

The stepwise method to solve this problem:

Step 1: Identify the velocity function.

The velocity function is
`\( v(t) = 4t - 6 \).`

Step 2: Find the time(s) when the velocity is zero.

This is necessary to determine when the particle changes direction. To find this, we set
`\( v(t) = 0 \).`

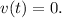
Step 3: Integrate the absolute value of the velocity function over the given interval.

This step will be divided into two parts if the velocity changes sign over the interval.

Step 4: Calculate the distance traveled.

The total distance is the sum of the absolute values of the definite integrals from step 3.

Let's start with step 1 and move through the process. We'll first find when the velocity is zero by solving
`\( 4t - 6 = 0 \).`

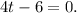
2: The velocity is zero at time
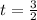`\( t = (3)/(2) \)` seconds. This indicates that the particle changes direction at
`\( t = 1.5 \)` seconds.

Step 3: Since the velocity function changes sign at
`\( t = 1.5 \)` seconds, we'll split the integral into two parts: from 0 to 1.5 seconds, and from 1.5 to 3 seconds.

Step 4: We will calculate the definite integral of the absolute value of the velocity function over these two intervals separately.

The velocity function is negative from
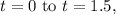`\( t = 0 \) to \( t = 1.5 \),` and positive from
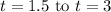`\( t = 1.5 \) to \( t = 3 \)`. Therefore, we take the absolute value of
`\( v(t) \)` accordingly.

Let's perform the integration stepwise for each interval.

Step 4:The total distance the particle travels over the time interval
`\([0,3]\) is \(9\) meters.`