Question

Pls help,I need this done by today.

Answer 1

Part (A)

We have two congruent right triangles with base and height of 5 and 3

Let's find the area of one triangle.

area = 0.5*base*height = 0.5*5*3 = 7.5

That's the area of one triangle.

Double it to get the total area of 2*7.5 = 15.

----------

Or another method is to use the area of a parallelogram formula

area = base*height

area = 3*5

area = 15

Answer: 15 square cm

====================================================

Part (B)

Focus on one of the four congruent right triangles.

Use the pythagorean theorem with a = 2 and b = 4 to find the hypotenuse c.

`a^2+b^2 = c^2\\\\c = √(a^2+b^2)\\\\c = √(2^2+4^2)\\\\c = √(20)\\\\`

The unshaded inner square has side lengths of
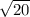`√(20)` centimeters.

The area of the unshaded inner region is
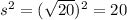`s^2 = (√(20))^2 = 20` square cm.

The entire square is 6 cm by 6 cm (since 2+4 = 6). This larger square has area 6^2 = 36

The shaded area is the difference of these two regions

36 - 20 = 16

--------

Another approach

area of triangle = 0.5*base*height

area = 0.5*2*4

area = 4

One shaded triangle has area 4 square cm. Quadruple this because we have 4 congruent right triangles with the same area as each other.

4*4 = 16 is the total shaded area

Answer: 16 square cm

====================================================

Part (C)

m = area of larger square

m = 5*5

m = 25 square cm

n = area of unshaded smaller square

n = 2*2

n = 4 square cm

p = shaded area

p = difference of m and n

p = m - n

p = 25 - 4

p = 21

Answer: 21 square cm