How many solutions does the following equation have? 3(y+41)=3y+123, Option 1: No solutions Option 2: Exactly one solution Option 3: Infinitely many solutions

Question

asked Oct 14, 2024 224k views

2 Answers

Wakakak · Answer 1 · 2024-10-16T11:42:49+0000

Answer: 3- infinitely many solutions

Explanation:

3(y+41)=3y+123

3×y+3×41=3y+123

3y+123=3y+123

0=0

This means this equation has infinite solutions.

Paul Lindner · Answer 2 · 2024-10-18T09:56:24+0000

Hello!

Answer:

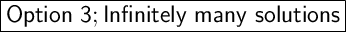
$\Large \boxed{\sf Option ~3; Infinitely~ many ~solutions}$

Explanation:

→ We want to solve this equation:

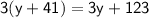
$\sf 3(y+41)=3y+123$

◼ Simplify the left side:

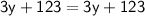
$\sf 3y+123=3y+123$

◼ Subtract 123 from both sides:

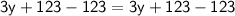
$\sf 3y+123-123=3y+123-123$

◼ Simplify both sides:

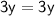
$\sf 3y=3y$

◼ Subtract 3y from both sides:

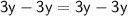
$\sf 3y-3y=3y-3y$

◼ Simplify both sides:

$\sf 0=0$

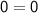
→ The expression entered is an identity: it is true for all values.

Conclusion:

The equation 3(y+41) = 3y + 123 has infinitely many solutions.

So the answer is the option 3.