Solve this please. Needs two answers |(2)/(3)x-5|\leq 3

Question

asked Apr 11, 2024 142k views

1 Answer

SnitramSD · Answer 1 · 2024-04-15T01:32:40+0000

Answer:

See below

Explanation:

We are given the following inequality:

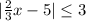
$|(2)/(3) x - 5 | \leq 3$

We want to solve it.

Recall that absolute value is the distance a value has from 0. It is always positive, so |3| is 3 and |-3| is also 3.

Also recall that |x| < 1 has two possible situations: x < 1 and x > -1.

This means that there are two possible situations: where
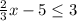$(2)/(3) x -5 \leq 3$ and where
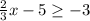$(2)/(3) x -5 \geq -3$ .

We can solve solve both of the situations:

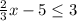
$(2)/(3) x -5 \leq 3$

Add 5 to both sides.

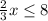
$(2)/(3) x \leq 8$

Multiply both sides by
(3)/(2) .

$x \leq 12$

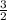Also:

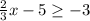
$(2)/(3) x -5 \geq -3$

Add 5 to both sides.

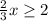
$(2)/(3) x\geq 2$

Now multiply both sides by
(3)/(2) .

$x\geq 3$

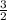Our answers are:
$x \leq 12$ and
$x\geq 3$ .