Question

Q55
Please help me as soon as possible.

Answer 1

`\cos \left[\csc^(-1)\left((b)/(a)\right)\right]=(√(b^2-a^2))/(b)`

Explanation:

The cosecant ratio (csc) is a trigonometric function that is the reciprocal of the sine function. While the sine ratio relates the length of the side opposite the angle to the hypotenuse in a right triangle, the cosecant ratio expresses the inverse relationship, so the ratio of the hypotenuse to the side opposite the angle.

`\csc \theta=(1)/(\sin \theta)=(1)/((\sf Opposite)/(\sf Hypotenuse))=(\sf Hypotenuse)/(\sf Opposite)`

Therefore:

`\csc \theta = \sf (Hypotenuse)/(Opposite)\implies \theta=\csc^(-1)\left(\sf (Hypotenuse)/(Opposite)\right)`

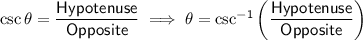
Given csc⁻¹(b/a), then side a is the side opposite the angle.

This means that the side adjacent the angle is the side labeled √(b² - a²).

`\cos \left[\csc^(-1)\left((b)/(a)\right)\right]=\cos \theta`

As the cosine ratio relates the length of the adjacent side to the hypotenuse, then:

`\cos \theta=(\sf Adjacent)/(\sf Hypotenuse)=(√(b^2-a^2))/(b)`

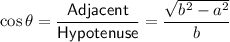
Therefore:

`\cos \left[\csc^(-1)\left((b)/(a)\right)\right]=(√(b^2-a^2))/(b)`