Answer:
![\cos \left[\csc^(-1)\left((b)/(a)\right)\right]=(√(b^2-a^2))/(b)](https://img.qammunity.org/2024/formulas/mathematics/college/sxqt8owhomk0t31u959siwm2bp1x4s25pp.png)
Explanation:
The cosecant ratio (csc) is a trigonometric function that is the reciprocal of the sine function. While the sine ratio relates the length of the side opposite the angle to the hypotenuse in a right triangle, the cosecant ratio expresses the inverse relationship, so the ratio of the hypotenuse to the side opposite the angle.

Therefore:
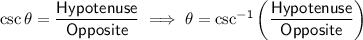
Given csc⁻¹(b/a), then side a is the side opposite the angle.
This means that the side adjacent the angle is the side labeled √(b² - a²).
![\cos \left[\csc^(-1)\left((b)/(a)\right)\right]=\cos \theta](https://img.qammunity.org/2024/formulas/mathematics/college/1efd5jjwnjosjxojh2ui97nv3sr150zskf.png)
As the cosine ratio relates the length of the adjacent side to the hypotenuse, then:
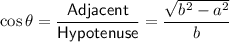
Therefore:
![\cos \left[\csc^(-1)\left((b)/(a)\right)\right]=(√(b^2-a^2))/(b)](https://img.qammunity.org/2024/formulas/mathematics/college/sxqt8owhomk0t31u959siwm2bp1x4s25pp.png)