Answer:
16.875
Explanation:

Given:
- Sum of infinite geometric series:
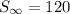
- Common ratio: r = 0.75
To find the value of the third term, we first need to find the value of the first term (a₁) by substituting the given values of
 and r into the sum of an infinite geometric series formula:
and r into the sum of an infinite geometric series formula:
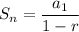
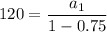
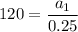
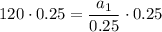
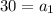
Therefore, the value of the first term is a₁ = 30.
Now we have found the first term, we can substitute the values of a₁ and r into the general equation of a geometric sequence.

Therefore, the nth term of the geometric sequence is:
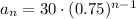
To find the value of the third term (a₃), we can substitute n = 3 into the nth term equation:
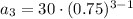
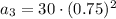
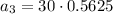
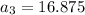
So, the third term of an infinite geometric series with a sum of 120 and a common ratio of 0.75 is 16.875.