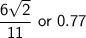Question

Q49
Please help me as soon as possible.

Answer 1

39.5°

Explanation:

First, find the length of DF using pythagorean theorem

let a be the length of line DF

11² - 7² = a²

121 - 49 = a²

72 = a²

a = 8.485...

cos F = adjacent/hypotenuse

cos F = 8.485.../11

cos F = 0.7713...

find the inverse of cos F

cos⁻¹ of 0.7713... = 39.5°

Answer 2

`\sf (6√(2))/(11) \textsf{ or } 0.77`

Explanation:

Given:

In right angled triangle DEF with respect to F

Opposite = ED = 7

Hypotenuse = EF = 11

Adjacent = DF

To find:

Value of cos F.

Solution:

The cos function is defined as the ratio of the adjacent side to the hypotenuse.

So, we have the equation:

`\sf cos F =( DF)/(EF)`

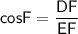
Over here, we do not have an adjacent DF.

We can find DF by using Pythagoras theorem:

which state that "square of hypotenuse is equal to the sum of square of two other sides" .

Using this:

We have:

`\sf EF^2 = ED^2 + DF^2`

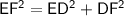
Substitute the given values:

`\sf 11^2 = 7^2+DF^2`

`\sf 121 = 49 + DF^2`

`\sf 121-49 = DF^2`

`\sf DF ^2 = 72`

`\sf DF =√(72)`

`\sf DF =6√(2)`

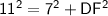
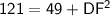
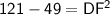
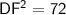
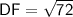
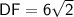
Substituting the values we have, we get:

`\sf cos F =( 6√(2))/(11)`

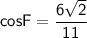
Therefore, the value of cos F is:

`\sf (6√(2))/(11) \textsf{ or } 0.77`