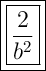Question

Q39
Please help me as soon as possible.

Answer 1

`\textsf{D.} \quad(2)/(b^2)`

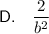
Explanation:

Given expression:

`(4b^(5))/(2b^(3) \cdot b^(4))\qquad \text{if}\;b > 1`

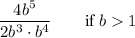
To simplify the given expression, we can use Laws of Exponents.

`\boxed{\begin{array}{rl}\underline{\sf Laws\;of\;Exponents}\\\\\sf Product:&a^m * a^n=a^(m+n)\\\\\sf Quotient:&(a^m)/(a^n)=a^(m-n)\\\\\end{array}}`

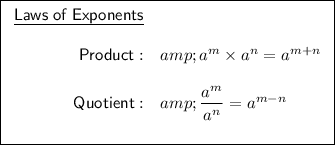
Simplify the denominator of the given expression by applying the product law of exponents:

`\begin{aligned}(4b^(5))/(2b^(3) \cdot b^(4))&=(4b^(5))/(2b^(3+4))\\\\&=(4b^(5))/(2b^(7))\end{aligned}`

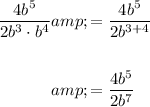
Divide the numbers 4 and 2:

`= (2b^(5))/(b^(7))`

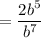
Apply the quotient law of exponents:

`\begin{aligned}&= 2b^(5-7)\\\\&=2b^(-2)\end{aligned}`

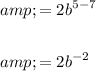
Apply the negative exponent law:

`=(2)/(b^2)`

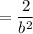
Therefore, the simplified expression given b > 1 is:

`\Large\boxed{\boxed{(2)/(b^2)}}`