Question

What is the wavelength of light with a frequency of 2.2x10^12 s^-1?

Answer 1

The wavelength of light with a frequency of 2.2x10^12 s^-1 is calculated using the wave equation and is found to be 1.36 × 10^5 nm.

Step-by-step explanation:

The question asks us to find the wavelength of light when its frequency is given as 2.2x1012 s-1. To calculate the wavelength (λ), we can use the formula λ = c / ν, where c is the speed of light (3.0 × 108 m/s) and ν (nu) is the frequency of the wave. Plugging in the values, we get:

λ = (3.0 × 108 m/s) / (2.2 × 1012 s-1) = 1.36 × 10-4 m.

To express the wavelength in nanometers (nm), we convert meters to nanometers by multiplying by 109 (since 1 m = 109 nm), yielding:

λ = 1.36 × 10-4 m × 109 nm/m = 1.36 × 105 nm.

Answer 2

The wavelength of light with a frequency of
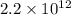`\(2.2 * 10^(12)\)` Hz is approximately 136.36 micrometers.

To calculate the wavelength of light with a frequency of
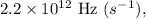`\(2.2 * 10^(12)\) Hz (\(s^(-1)\)),`we use the relationship between wavelength
`(\(\lambda\)),` frequency (f), and the speed of light (c). The speed of light in a vacuum is a constant,
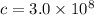`\(c = 3.0 * 10^8\)`meters per second (m/s).

The formula to relate these quantities is:

`\[ c = \lambda * f \]`

Where:

- c is the speed of light (about
`\(3.0 * 10^8\) m/s),`

-
`\(\lambda\)` is the wavelength (which we are trying to find),

- f is the frequency
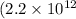`(\(2.2 * 10^(12)\)`Hz in this case).

Rearranging this formula to solve for the wavelength
`(\(\lambda\))`, we get:

`\[ \lambda = (c)/(f) \]`

Let's calculate the wavelength using this formula.

The wavelength of light with a frequency of
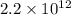`\(2.2 * 10^(12)\)` Hz is approximately 0.000136 meters, or 136.36 micrometers.