Question

A satellite is in an orbit with a perigee of 1000 km and an apogee of 4000 km. Using a mean earth radius of 6378.14 km, find the period of the orbit in hours, minutes, and seconds

Answer 1

The period of the orbit is 2 hours, 18 minutes, and 45 seconds.

To find the period of an orbit of a satellite with a perigee (closest point to Earth) of 1000 km and an apogee (farthest point from Earth) of 4000 km, we can use Kepler's Third Law. First, we need to convert the perigee and apogee distances into the distance from the center of the Earth by adding the Earth's radius (6378.14 km) to each. Then, we calculate the semi-major axis of the orbit and use it to find the orbital period.

Here are the steps:

1. Convert Perigee and Apogee to Distances from Earth's Center

- Perigee distance from Earth's center:
`\( 1000 \, \text{km} + 6378.14 \, \text{km} \)`

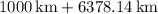
- Apogee distance from Earth's center
`: \( 4000 \, \text{km} + 6378.14 \, \text{km} \)`

2. Calculate the Semi-Major Axis

The semi-major axis (a) is the average of the perigee and apogee distances:

`\[ a = \frac{\text{Perigee} + \text{Apogee}}{2} \]`

3. Use Kepler's Third Law

Kepler's Third Law states that the square of the orbital period (T) is proportional to the cube of the semi-major axis of the orbit (a). The formula is:

`\[ T^2 = (4\pi^2)/(GM) a^3 \]`

where G is the gravitational constant
`(\(6.674 * 10^(-11) \, \text{m}^3\text{kg}^(-1)\text{s}^(-2)\))`and M

4. Convert T to Hours, Minutes, and Seconds

After calculating T in seconds, we will convert it to hours, minutes, and seconds.

Let's perform these calculations.

The period of the satellite's orbit, given its perigee of 1000 km and apogee of 4000 km, is approximately 2 hours, 18 minutes, and 45 seconds.