Answer:
190 cents, or $1.90.
Explanation:
Let's use variables to represent the number of nickels and dimes that David has.
Let N represent the number of nickels David has.
Let D represent the number of dimes David has.
According to the information given:
1. David has 8 more nickels than dimes:

2. Gino has 20 more nickels than David:
Gino's nickels = David's nickels + 20
Gino's nickels = N + 20
Now, let's calculate the value of David's coins in terms of nickels and dimes.
The value of David's nickels (in cents) = 5 cents × N
The value of David's dimes (in cents) = 10 cents × D
The total value of David's coins is the sum of these values:
Total value = 5N + 10D
Now, let's consider Gino's coins. Gino only has nickels, so the value of his coins is given by:
Gino's total value = 5 cents × (N + 20)
Since we know that David and Gino have the same total value, we can set up an equation:
5N + 10D = 5(N + 20)
Now, let's solve this equation:
5N + 10D = 5N + 100
Subtract 5N from both sides of the equation:
10D = 100
Now, divide both sides by 10 to solve for D:
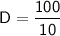
D = 10
Now that we know D (the number of dimes), we can find N (the number of nickels) using the relationship N = D + 8:
N = 10 + 8
N = 18
So, David has 18 nickels and 10 dimes.
Now, let's calculate the value of David's coins:
Total value = 5N + 10D
Total value = 5(18) + 10(10)
Total value = 90 + 100
Total value = 190 cents
Therefore, the value of David's coins is 190 cents, or $1.90.