Question

Y=x²+8x-10 p is the turning point of the curve work out the coordinates of p

Answer 1

(-4, -26)

Explanation:

The vertex of a parabola in the form:

`y = ax^2 + bx + c`

has the coordinates:

`\left(-(b)/(2a),\ -(b^2)/(4a) + c\right)`

We can find the vertex of the given parabola:

`y=x^2+8x-10`

by identifying the values for
`a`,
`b`, and
`c`, then plugging those into the vertex coordinates formula:

• 
  `a=1`
• 
  `b=8`
• 
  `c=-10`

↓ plugging these into the formula

`\left(-(8)/(2(1)), \ -(8^2)/(4(1)) + (-10)\right)`

↓ simplifying

`\left(-4, \ -(64)/(4) -10\right)`

`(-4,\ -16-10)`

`\boxed{(-4, -26)}`

Answer 2

p = (- 4, - 26 )

Explanation:

given a quadratic in standard form

y = ax² + bx + c ( a ≠ 0 ) , then

the x- coordinate of the turning point is

x = -
`(b)/(2a)`

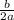
y = x² + 8x - 10 ← is in standard form

with a = 1 and b = 8 , then x- coordinate of turning point is

x = -
`(8)/(2)` = - 4

substitute x = - 4 into the quadratic for corresponding y- coordinate

y = (- 4)² + 8(- 4) - 10 = 16 - 32 - 10 = - 26

coordinates of p are (- 4, - 26 )