Question

Use completing the square to find the roots of the following equation. 3x2 - 24x=-9

Answer 1

Explanation:

"Completing the square" is a method used for quadratic equations, so let's first put this question into the standard quadratic equation form:

`ax^(2) + bx + c = 0` -->
`3x^(2) - 24x + 9 = 0`

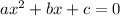See all the factors of 3? Let's divide both sides by 3 to clean that up:

`x^(2) - 8x + 3 = 0`

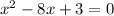
It's the same equation/equality, just a lot cleaner. And you need a = 1 for this to work.

Now we have to find the formula for completing the square:

(x + b/2)² = -(c - b²/4)

You don't have to memorize that, it's in your textbook or course notes somewhere. I had to look it up on the interwebs.

Now just plug in the b's and c's we know:

(x - 8/2)² = -(3 - (-8)²/4)

(x - 4)² = -(3 - 16)

(x - 4)² = 13

(x-4) =
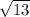`√(13)` Then getting x by itself:

x = 4 ±
`√(13)`

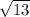
So x = 4 +
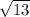`√(13)` AND x = 4 -
`√(13)`

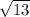
I didn't think I'd end up with that kind of answer, but I can't find an error in what I did; maybe you can. Did you write the equation correctly, especially the signs? Especially on the "-9" term? It would work out to x = 1 & 9 if that -9 was a +9.