Question

The number of vacancies in some metal at 879 C is 1.9 x 10²⁴ m³. Calculate the number of vacancies at 646 C given that the energy of vacancy formation is 1.09 ev/atom ; assume the density at both temp

Answer 1

The number of vacancies at 646°C is approximately 1.28 x 10²⁴ m³.

How to calculate the number of vacancies?

Convert temperatures to Kelvin:

T₁ = 879°C + 273.15

T₁ = 1152.15 K

T₂ = 646°C + 273.15

T₂ = 919.15 K

Calculate the change in free energy:

`\Delta F = E_f * (k_B * (T_1 - T_2))`

`\Delta F = 1.09 eV/atom * (8.617 * 10^(-5) eV/K * (1152.15 K - 919.15 K))`

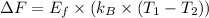
ΔF ≈ 0.63 eV/atom

Calculate the ratio of vacancy concentrations:

`n_2 / n_1 = exp(-\Delta F / (k_B * T_2))`

`n_2 / 1.9 * 10^(24) m^(3) = exp(-0.63 eV/atom / (8.617 * 10^(-5) eV/K * 919.15 K))`

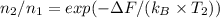
`n_2` ≈ 1.28 x 10²⁴ m³

Therefore, the number of vacancies at 646°C is approximately 1.28 x 10²⁴ m³.

Complete question:

The number of vacancies in some metal at 879 C is 1.9 x 10²⁴ m³. Calculate the number of vacancies at 646 C given that the energy of vacancy formation is 1.09 ev/atom ; assume the density at both temperatures is the same.