Question

Scientists observed that a small colony of penguins on a remote Antarctic island obeys the population growth law. There were 2000 penguins initially and 2400 penguins 18 months later. How long will it take for the number of penguins to double? (a) 6.35 years (b) 5.97 years (c) 5.12 years (d) 5.70 years (e) None of the above.​

Answer 1

(d) 5.70 years

Explanation:

To determine how long it will take for the population of penguins to double, we can use the population growth formula.

Population Growth formula

`\large\boxed{P(t) = P_0 \cdot e^(rt)}`

where:

• P(t) is the population at time t.
• P₀ is the initial population.
• r is the growth rate.
• t is the time in years.
• e is Euler's constant.

We are given that there were 2000 penguins initially, and 2400 penguins 18 months later. Therefore:

• P = 2400
• P₀ = 2000
• t = 1.5 years (18 months)

Substitute these values into the formula and solve for r:

`\begin{aligned}2400 &= 2000 \cdot e^(1.5r)\\\\ 1.2&=e^(1.5r)\\\\\ln(1.2)&=\ln\left(e^(1.5r)\right)\\\\\ln(1.2)&=1.5r\ln(e)\\\\\ln(1.2)&=1.5r\\\\r&=(\ln(1.2))/(1.5)\end{aligned}`

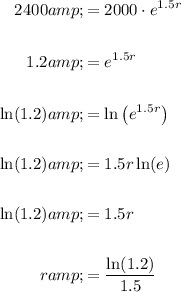
Now that we have the growth rate (r), we can find out how long it will take for the population to double:

`2 \cdot 2000 = 2000 \cdot e^{(\ln(1.2))/(1.5)t}`

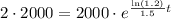
Solve for t:

`\begin{aligned}2&=e^{(\ln(1.2))/(1.5)t}\\\\\ln(2)&=e^{(\ln(1.2))/(1.5)t}\\\\\ln(2)&=\ln\left(e^{(\ln(1.2))/(1.5)t}\right)\\\\\ln(2)&=(\ln(1.2))/(1.5)t\ln(e)\\\\\ln(2)&=(\ln(1.2))/(1.5)t\\\\t&=(1.5\ln(2))/(\ln(1.2))\\\\t&=5.702676025...\\\\t&=5.70\; \sf years\;(2\;d.p.)\end{aligned}`

So, it will take approximately 5.70 years for the number of penguins to double.