Question

The 21st term of AP whose first two terms are -3 and 4 is:

(a) 17
(b) 137
(c) 143
(d) -143​

Answer 1

(b) 137

Explanation:

An arithmetic progression (AP) is a sequence of numbers where the difference between any two consecutive terms is constant. This constant difference is called the common difference.

In this case:

The nth term of an arithmetic progression can be calculated using the following formula:

`\sf t_n = a + (n - 1) * d`

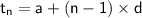
where:

• tn is the nth term of the AP
• a is the first term of the AP
• d is the common difference of the AP
• n is the number of the term

We have,

• First term (a)= -3
• The common difference (d)= 7

So, the 21st term can be calculated by substituting given value in above formula:

`\begin{aligned} t_(21 ) &\sf = -3 + (21 - 1) * 7 \\\\ &\sf -3 +20* 7 \\\\ &\sf = -3+ 140 \\\\ &\sf = 137\end{aligned}`

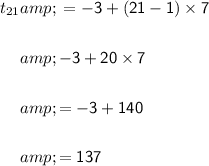
Therefore, the answer is (b) 137