Question

Find the coordinates of the other endpoint of the​ segment, given its midpoint and one endpoint.​ (Hint: Let​ (x,y) be the unknown endpoint. Apply the midpoint​ formula, and solve the two equations for x and​ y.) midpoint (6,10) endpoint (15,17)

Answer 1

(-3, 3)

Explanation:

Given:

Midpoint = (6, 10)

Endpoint 1 = (15, 17)

The midpoint formula:

M(x, y) =
`((x_(1) + x_(2))/(2), (y_(1) + y_(2))/(2))`

Where (x1, y1) represent one pair of coordinates and (x2, y2) represent the other pair. The (x, y) in the beginning stands for the x - value of the midpoint and y - value of the midpoint.

So to solve for a missing endpoint given the midpoint and the other endpoint, we just have to apply this formula.

Let's plug in what we have into this.

Since we know the x and y values of the midpoint (6, 10), we'll make two equations setting one to x(6) and the other to y(10).

Then, we substitute one of the x-values (in the numerator) for the first equation to the x - value of the given endpoint(15) and solve for x. For the second equation, we set one of the y-values(in the numerator) to the y - value of the given endpoint(17) and solve for y.

Let's set these equations up,

First let's solve for the x - value of the endpoint:

(we substitute one x - value in the numerator for the x - value of the given endpoint which is 15, then we set the whole equation to equal 6 since that is the midpoint's x - value and we are trying to solve for the x - value of the endpoint.)

`(15 + x_(2))/(2) = 6`

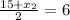
(we are basically averaging)

Multiply both sides by 2 (inverse property of division is multiplication):

15 + x2 = 12

Subtract 15 from both sides (inverse property of addition is subtraction):

x2 = -3

The endpoint's x - value is -3.

Now let's solve for the y - value of the endpoint:

(we substitute one y - value in the numerator for the y - value of the given endpoint which is 17, then we set the whole equation to equal 10 since that is the midpoint's y - value and we are trying to solve for the y - value of the endpoint.)

`(17 + y_(2))/(2) = 10`

Multiply both sides by 2 (inverse property of division is multiplication):

17 + y2 = 20

Subtract 17 from both sides (inverse property of addition is subtraction):

y2 = 3

The endpoint's y - value is 3.

Now, let's put what we found together in a coordinate format:

(x, y)

= (-3, 3)

The other endpoint is (-3, 3).

Answer 2

(-3,3)

Explanation: