Question

Karissa is a college basketball player who makes 85% of her free throws. In a recent game, she had 8 free throws and missed 3 of them. Using software, a calculator, or Table C, compute 1−P(X≤2), where X is the number of free throws missed in 8 shots. Give your answer to four decimal places. 1−P(X≤2)= Do you consider this outcome unusual? Explain your answer. This outcome because the probability that Karissa missed 3 or more throws is than

Answer 1

To compute 1−P(X≤2), where X is the number of free throws missed in 8 shots, we need to calculate the probabilities using the binomial probability formula and summing the probabilities of missing 0, 1, and 2 free throws.

Step-by-step explanation:

To compute 1−P(X≤2), where X is the number of free throws missed in 8 shots, we need to first calculate the probability of missing 0, 1, or 2 free throws. Since Karissa makes 85% of her free throws, the probability of missing a free throw is 1 - 0.85 = 0.15. Now we can calculate the probabilities using the binomial probability formula:

`P(X=k) = C(n,k) * p^k * (1-p)^(n-k)`

`P(X=0) = C(8,0) * 0.15^0 * (1-0.15)^(8-0)`

`P(X=1) = C(8,1) * 0.15^1 * (1-0.15)^(8-1)`

`P(X=2) = C(8,2) * 0.15^2 * (1-0.15)^(8-2)`

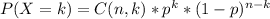
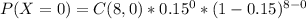
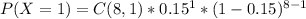
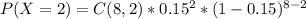
Then we can calculate P(X≤2) by summing the probabilities of missing 0, 1, and 2 free throws. Finally, subtracting it from 1 will give us the value of 1−P(X≤2).