Question

Find the value of Z 96 I will give 42 points pls yeah​

Answer 1

`z\° = 48\°`

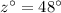
Explanation:

We can solve for the measure of angle z using:

• the definition of supplementary angles
• the Isosceles Triangle Theorem

First, we can solve for the measure of the angle that is supplementary to 96°. We know that the measures of supplementary angles add to 180°. Hence, we can form the equation to solve for the supplement (x°):

`96\° + x\° = 180\°`

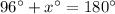
↓ subtracting 96° from both sides

`x\° = 84\°`

Next, we can solve for the measure of angle z using the fact that the measures of the interior angles of a triangle add to 180°, as well as the Isosceles Triangle Theorem, which tells us that the base angles of an isosceles triangle are congruent, and therefore, the bottom angle in this diagram is the same measure as z°. Here is the equation that models this situation:

`2(z\°) + x\° = 180\°`

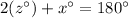
↓ substituting in the value of x

`2(z\°) + 84\° = 180\°`

↓ subtracting 84° from both sides

`2(z\°) = 96\°`

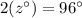
↓ dividing both sides by 2

`\boxed{z\° = 48\°}`